Equação Vetorial da Reta

     Suponha que exista um ponto conhecido A de coordenadas (x1, y1, z1) e um ponto qualquer P (x, y, z). Há um vetor não - nulo AP que sai de A e vai para P e um vetor v (a,b,c) paralelo a AP e, portanto, de mesmos sentido e direção. Esse vetor v  parte da origem e é denominado vetor diretor da reta r que passa pelos pontos A e P, recebe esse nome pelo fato de definir a direção da reta. (1)

Figura 1 - Reta r 

Retirada de (1)

     Para que P pertença a reta r é necessário que v e AP sejam linearmente dependentes, ou seja: (2)

     AP = tv.

     Como AP = P - A, tem-se que P - A = tv ou P = A + tv  portanto:

     (x , y, z) = (x1, y1, z1) + t (a, b, c).

     Exemplo 1: 

     Determinar a equação vetorial da reta r que passa pelo ponto A (3,0, 5) e tem a direção do vetor v = 2i + 2j - k:

     Substituindo na equação, tem-se: r: (x, y, z) = (3,0,5) + t(2,2,-1).

     Exemplo 2 : 

     Determinar a equação vetorial da reta s que passa por A (1,-1,4) e tem a direção de v (2,3,2) :

     A partir da equação é possível obter: (x, y, z) = (1,-1,4) + t(2,3,2).

Referências:

1 - STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987.

Observação: os vetores estão representados em negrito.

Equações Paramétricas da Reta

     Para um ponto conhecido A (x1, y1, z1), um ponto qualquer P (x, y, z) e um vetor diretor v (a, b, c) tem-se a equação vetorial da reta dada por: (1)

     P = A + tV ou (x , y, z) = (x1, y1, z1) + t (a, b, c). Desenvolvendo essa equação, tem-se:

     (x , y, z) = (x1, y1, z1) + (ta, tb, tc), (x, y, z) = (x1 + ta, y1 + tb, z1 +tc).

     Assim:

     x = x1 + at; y = y1 + bt; z = z1 + ct.

     Tais equações são denominadas equações paramétricas da reta. (1)

     Exemplo 1:

     Escreva as equações paramétricas da reta que passa por A (3,-4,2) e é paralela ao vetor v (2,1,-3):

     Temos que: x1 = 3 e a = 2; y1 = -4 e b = 1; z1 = 2 e c = -3. 

     Assim: x = 3 + 2t; y = -4 + t; z = 2 - 3t.

     Exemplo 2:

     Determinar o ponto P da reta que tem abscissa 4:

    Pode-se substituir o valor fornecido para x para encontrar o valor de t e, assim, encontrar os valores de y e de z: 4 = 2 -t; 4-2 = -t; t= -2.

     Assim pode-se achar o valor de y: y = 3 - 2, y = 1. Pode-se também encontrar o valor de z:

     z = 1 -2(-2), z= 1 +4, z = 5.

     Conclusão: temos que P = (4, 1, 5).

Referências:

1 - STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987.

Observação: os vetores estão representados em negrito.

Reta Definida por 2 Pontos

     Quando são fornecidos dois pontos conhecidos da reta A (x1, y1, z1) e B (x2,y2, z2), é possível obter o vetor diretor v da reta para então equacionar essa reta r. O vetor v = AB = B-A.                Assim: (1)

     v = (x2 - x1, y2 -y1, z2 - z1)

     Dessa forma, a equação da reta r é:

     (x, y, z) = (x1, y1, z1) + t(x2 - x1, y2 - y1, z2 - z1) ou

     (x, y, z) = (x2,y2, z2) + t(x2 - x1, y2 - y1, z2 - z1) ou ainda:

     x = x1 + (x2 - x1)t; y = y1 + (y2 -y1)t; z = z2 + (z2 - z1)  

  

     Exemplo 1: 

     Escreva as equações paramétricas da reta definida pelos pontos A(1,1,1) e B (2,3,5) : 

     Deve-se encontrar o vetor diretor primeiro para, depois, obter a equação da reta

     v = B -A = (2-1, 3-1, 5-1), v = (1, 2, 4)    = vetor diretor.

     P = B + tv.     

     x = 2 +1t; y= 3 + 2t; z = 5+ 4t.

     Conclusão:  a reta r é representada por : (x, y, z) = (2, 3, 5) + t( 1, 2, 4).

     Exemplo 2:

     Determinar as equações paramétricas da reta r que passa pelo ponto A (1, -2, -3) e B (3, 1, -4):

     v = (3 - 1, 1 + 2, -4 + 3), v = (2, 3, -1).

     x = 1 + 2t; y = -2 + 3t; z = -3 -t.

Referências:

1 - STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987.

Observações: os vetores estão representados em negrito.

Equações Simétricas da Reta

     As equações simétricas são obtidas a partir das equações paramétricas. Tem-se que as paramétricas são definidas por: (1)

     x = x1 + at; y = y1 + bt; z = z1 + ct.                

     Isolando o parâmetro (t) em cada equação, tem-se:

     t=(x - x1)/a; t =  (y - y1 )/b; t =  (z - z1 )/c.

     Desse modo: (x - x1)/a = (y - y1 )/b = (z - z1 )/c

    Tais equações são denominadas equações simétricas, ou normais, da reta r que passa pelo ponto conhecido A (x1, y1, z1) , por um ponto qualquer P (x, y, z) e tem o vetor v (a, b, c) como vetor diretor. (1)

     Observação: 

     Para obter as equações simétricas da reta é necessário que o produto abc seja diferente de zero, isto é: abc ≠ 0 (1)

     Exemplo 1 :

     Obter as equações simétricas da reta que passa pelo ponto A (3,0,5) e tem direção do vetor v (2, 2, -1):

     Substituindo (2,2,-1) no lugar de (a, b,c) e (3, 0,5) em (x1, y1, z1), obtemos as equações da reta

(x-3)/2  =  (y-0 )/2=  (z-(-5) )/(-1).

     Conclusão: as equações simétricas da reta são:(x-3)/2  = (y )/2  = (z+5 )/(-1)

  

     Exemplo 2:

     Determinar os pontos da reta r: (x-3)/2 = (y+1)/(-1) = z/(-2) que têm a) abscissa 5; b) ordenada 4; c) cota 1.

• a) Como x=5: (5-3)/2  = 1. Assim, pode-se calcular o valor de y:

     1 = (y +1)/(-1), y = -2. Também é possível calcular z:

     1 = z/(-2), z = -2.

     Conclusão: para abscissa 5, tem-se o ponto P (5, -2, -2)

• b) Como y = 4: (4+1)/(-1) = -5. Assim, pode-se calcular o valor de x:

     -5 = (x-3)/2, x= -7. Pode-se encontrar também o valor de z:

     -5 = z/(-2), z = 10.

     Conclusão: para ordenada 4, tem-se o ponto P (-7, 4, 10).

• c) Como z = 1: 1/(-2) = - -1/2. Assim, pode-se calcular o valor de x:

      - -1/2 = (x-3)/2, x = 2. Pode-se também encontrar o valor de y:

      - -1/2 = (y +1)/(-1), y = - -1/2 .

     Conclusão: para cota 1, tem-se o ponto P (2, - -1/2 , 1).

Referências:

1 - STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987

Observação: os vetores estão representados em negrito.

Equações Reduzidas da Reta

     A partir das equações simétricas da reta é possível obter as equações reduzidas. Para tanto, deve-se isolar duas variáveis e deixá-las em função da terceira. Para uma reta r que passa pelo ponto conhecido A (x1, y1, z1) e tem V (a,b,c) como vetor diretor tem-se: (1)

     (x - x1)/a = (y - y1 )/b = (z - z1 )/c. Isolando y e z em função de x, tem-se:

•      Para y:

     (x - x1)/a = (y - y1 )/b. Logo, y - y1 = b/a ( x - x1) e y = bx/a - bx1/a + y1.

     Adotando: b/a = m ; - bx1/a + y1 = n, tem-se que: y = mx + n.

•      Para z:

     z - z1 = c/a (x - x1). Logo, z = cx/a - cx1/a + z1.

   Adotando: c/a = p ; - cx1/a + z1 = q, tem-se que: z = px +q. Portanto, as equações reduzidas da reta r na variável x são:

     y = mx + n

     z = px +q     

   

     Observação: 

     Há dois métodos de obter-se o vetor diretor a partir das equações reduzidas da reta: (2)

     a) Encontrar 2 pontos A e B da reta e obter o vetor AB = B - A. Este vetor AB é o vetor diretor. (2)

     b) Para as equações reduzidas na variável , isolar o x e obter as equações na forma simétrica. (2)

     Exemplo 1:

    Obter as equações reduzidas na variável x da reta que passa por A (2, -4, -3) e tem o vetor diretor v (1, 2, -3):

     y = mx + n, em que m = b/a e n = - bx1/a + y1

     m = 2/1 = 2; n = (-2.2)/1 -4 = -8. Logo, y = 2x -8.

     z = px + q, em que : p = c/a ; q = - cx1/a + z1.

     p = (-3)/1 = -3; q = (-(-3).2)/1 -3 = 3. Logo, z = -3x +3.

     Conclusão: a reta tem equações reduzidas: y = 2x -8 e z = -3x +3.

     Exemplo 2: 

     Obter o vetor diretor V (a, b, c) da reta cujas equações reduzidas são:

     y = 2x -8 e z= 5x/2 - 13.

     Deve-se isolar x e obter as equações simétricas:

     y  + 8 = 2x, então, x = (y+8)/2.

     z + 13 = 5x/2, então, z = (2z+26)/5.

     Assim, tem-se que as equações simétricas são: x/1=  (y+8)/2=(2z+26)/5.

     Conclusão: o vetor diretor V = (1, 2, 5)

Referências:

1 - STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987

2 - Apostila de Geometria Analítica - Retas. UNESP

Observações: os vetores estão representados em negrito.

Retas paralelas aos planos e aos eixos coordenados

     Considerando uma componente do vetor diretor igual à zero, que é representado pelo vetor v = (a, b, c) obteremos o vetor v ortogonal a um dos eixos coordenados, sendo então a reta r (determinada por um ponto A( x1, y1, z1)) paralela ao plano dos outros eixos. Portanto se: a = 0, v = (0,b,c), logo, é é perpendicular ao eixo "ox" e paralelo ao eixo "yoz".
     As equações da reta r ficam:

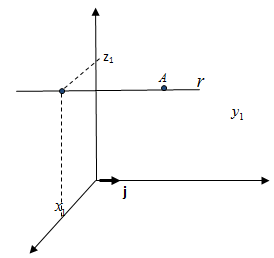
     Verificamos que a coordenada x permanece constante, variando somente entre y e z. Com isso averiguamos que a reta r se localiza num plano paralelo ao plano coordenado yOz. Como exemplo temos a ilustração abaixo:

Ilustração 1: Demonstração de plano paralelo ao plano coordenado yOz

Fonte: Retirado de (1)

     Caso a componente b do vetor diretor venha ser nulo obteremos: b = 0, v = (a,0,c), logo, é perpendicular ao eixo "oy" e paralelo ao eixo "xoz".
     As equações da reta ficam:

     Verificamos que a coordenada y permanece constante, variando somente entre x e z. Com isso averiguamos que a reta r se localiza num plano paralelo ao plano coordenado xOz.

Ilustração 2: Demonstração de plano paralelo ao plano coordenado xOz

Fonte: Retirado de 1

     Caso a componente c do vetor diretor venha ser nulo: c = 0, v = (a,b,0), logo, é perpendicular ao eixo "oz" e paralelo ao eixo "xoy".
     As equações da reta ficam:

    Verificamos que a coordenada z permanece constante, variando somente entre x e y. Com isso averiguamos que a reta r se localiza num plano paralelo ao plano coordenado xOy.

Ilustração 3: Demonstração de plano paralelo ao plano coordenado xOy

Fonte: Retirado de (1)

     Agora verificaremos quando duas das componentes de v são nulas.
     Caso as componentes ‘a’ e ‘b’ do vetor diretor forem nulos: v = (0,0,c)
     As equações da reta ficam:

     Verificamos que a coordenada z é variável.
 

Ilustração 4: Demonstração de coordenada z é variável

Fonte: Retirado de 1

     Caso os componentes ‘a’ e ‘c’ do vetor diretor forem nulos: v = (0,b,0)
     As equações da reta ficam:

     Verificamos que a coordenada y é variável.                                
     

                     

Ilustração 5: Demonstração de coordenada y é variável

Fonte: Retirado de 1

     Caso os componentes ‘b’ e ‘c’ do vetor diretor forem nulos: v = (a,0,0)
     As equações da reta ficam:

     Verificamos que a coordenada x é variável.

                         

Ilustração 6: Demonstração de coordenada x é variável

Fonte: Retirado de 1

     Exemplo: 

     Determinar as equações da reta que passa pelo ponto A (-2, 3, -2) e tem a direção do vetor v = 3i + 2k.
     Resolução:
     Com base na equação do vetor (3i + 2k) verificamos que as componentes do vetor v são: a = 3; b = 0 e  c = 2. Como a componente b é nula, verificamos que a reta se encontra num plano paralelo ao xOz, com as seguintes equações:

Referências:
http://www.matematica.pucminas.br/profs/web_fabiano/calculo1/lineares.pdf
http://www.pucrs.br/famat/augusto/alga/Alga0402.pdf
1 STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;
2 Retas. Disponível http://www.pucrs.br/famat/augusto/alga/Alga0402.pdf
Observações: os vetores estão representados em negrito.

Ângulo de duas retas

     É o menor ângulo formado por dois vetores diretores das retas.

  Ilustração 1: Demonstração de menor ângulo formado por dois vetores

Fonte: Retirado de 2

    Sendo θ este ângulo, temos:

     Exemplo:

     Calcular o ângulo entre as retas r1 e r2

     Os vetores que definem as direções das retas são:
     r1= v1= (1, 1, -2) r2 = v2= (-2 , 1, 1)
     Resolução:
     Substituiremos os valores na fórmula dada acima.

     Logo temos:

     Concluímos que o menor ângulo formado é de 60°

• Condições de paralelismo de duas retas:

     Para duas retas r1 e r2 serem paralelas, deve-se possuir a mesma condição da dos vetores v1 = (a1, b1, c1) e v2 = (a2, b2, c2)  que indicam as direções das retas. Isto é: a1/a2 =  b1/b2 =  c1/c2

     Exemplo:

     A reta r1, que passa pelos pontos A1(-3, 4, 2) e B1(5, -2, 4), e a reta r2 passa pelos seguintes pontos A2(-1, 2, -3) e B2( -5, 5, -4).
     A direção de r1 é dada pelo seguinte vetor v1= (8, -6, 2), r2 é dada pelo vetor v2= (-4, 3, -1)
     A condição de paralelismo de duas retas é: 8/(-4) = (-6)/3 = 2/(-1), o que prova serem paralelas as retas r1 e r2.

• Condições de ortogonalidade de duas retas:

     Para duas retas r1 e r2 serem ortogonais, deve-se possuir a mesma condição da dos vetores v1 =(a1, b1, c1) e v2 = (a2, b2, c2)  que indicam as direções das retas. Isto é: v1 * v2 = 0

     Exemplo:

     A direção de r1 é dada pelo seguinte vetor v1 = (8, 0, -6), e r2 é dada pelo vetor v2 = (3, 5, 4).
     A condição de ortogonalidade de duas retas é: v1 * v2 = 0
     Neste caso obtemos: (8, 0, -6). (3, 5, 4)= 24 + 0 - 24 = 0, o que prova serem ortogonais as retas r1 e r2.


Referências:
http://www.matematica.pucminas.br/profs/web_fabiano/calculo1/lineares.pdf
http://www.pucrs.br/famat/augusto/alga/Alga0402.pdf
1 STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;
2 Retas. Disponível http://www.pucrs.br/famat/augusto/alga/Alga0402.pdf
Observações: os vetores estão representados em negrito; * corresponde a produto interno entre vetores.

Condição de coplanaridade de duas retas

     Temos duas retas, r1 que passa pelo ponto A1 (x1, y1, z1) e possui o vetor v1 = (a1, b1, c1) indicando a sua direção  e r2 que passa pelo ponto A2 (x2, y2, z2) e possui o vetor v2 = (a2, b2, c2) indicando sua direção. As retas são ditas coplanares se v1, v2 e A1, A2 forem coplanares, isto é, se o produto misto de (v1, v2 , A1, A2) for nulo.

Ilustração 1: Demonstração de coplanaridade de duas retas

Fonte: Retirado de (1)

     Exemplo:

     As retas: r1: {(x-2)/2= y/3= (z-5)/4}; r2: {(x+5)/(-1)= (y +3)/1= (z-6)/3}
     A direção de r1 é dada pelo vetor v1= (2, 3, 4) que passa pelo ponto A1(2, 0, 5).
     A direção de r2 é dada pelo vetor  v2= (-1, 1, 3) que passa pelo ponto A2(-5, -3, 6)
     O vetor determinado pelos pontos A1 e A2 é A1A2 = (-7, -3, 1)
     Para as retas serem coplanares é necessário que seja nulo o produto misto (v1, v2 , A1, A2), sendo assim:

Ilustração 9: Matriz para cálculo do produto misto

Fonte: Autoria própria

     Ao calcularmos o determinante obtemos: 2 – 63 + 12 + 28 + 18 + 3= 0. Como o produto misto é nulo, provamos que as retas r1 e r2 são coplanares.

Referências:
http://www.matematica.pucminas.br/profs/web_fabiano/calculo1/lineares.pdf
http://www.pucrs.br/famat/augusto/alga/Alga0402.pdf
1 STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;
2 Retas. Disponível http://www.pucrs.br/famat/augusto/alga/Alga0402.pdf
Observações: os vetores estão representados em negrito.

Posições Relativas de Duas Retas

     São quatro as possibilidades para duas retas r e s de  : serem coplanares (concorrentes, paralelas distintas, paralelas coincidentes), reversas. (1)
     Coplanares, isto é, situadas no mesmo plano:

• Concorrentes: r ∩ s = I (I é o ponto de interseção das retas r e s)

          Ilustração 1 : Retas concorrentes

          Fonte: retirada de (2)

• Paralelas distintas: r ∩ s = ∅   ( ∅ é o conjunto vazio)

                    

Ilustração 2 : retas paralelas

Fonte : retirada de (2)

• Paralelas coincidentes: r ∩ s  = r = s

     Reversas: não situadas no mesmo plano. Nesse caso: r ∩ s = ∅  . (2)

Ilustração 3 : retas reversas

Fonte: retirada de (2)

     Considerando que  r é um vetor diretor de r e s é um vetor diretor de s e A e B são, respectivamente, pontos de r e s: (1)

• r e s serão reversas se, e somente se, (r, s, AB) são linearmente independentes (ilustração 4a). (r,s,AB) ≠ 0. (1) 
•    Equivalentemente, r e s são coplanares se, e somente se, (r, s, AB) são linearmente dependentes (inclui os casos de concorrentes, paralelas distintas, paralelas coincidentes); (r,s,AB) = 0. (1) 
• r e s serão paralelas se, e somente se, (r,s) são linearmente dependentes; (1)
• r e s serão concorrentes se, e somente se, são coplanares e não paralelas, isto é, (r, s, AB) são linearmente dependentes e  (r,s) são linearmente independentes (ilustração 4b)¹

Ilustração 4: retas reversas e retas coplanares

Fonte: retirado de (1)

     Exemplo: 

     Estudar a posição relativa das retas: (2)

     Solução

     São vetores diretores de r1 e r2 : v1 = (1,2,-1) e v2 = (-3,6,3)  . Como v2 = -3 v1 , as retas  r1 e r2 são paralelas e não coincidentes (basta ver que o ponto A1 = (0,-3,0) pertence a r1 e não pertence a r2).

Referências

(1) CAMARGO, Ivan de; BOULOS, Paulo. Geometria Analítica. -- 3ªed. rev e ampl -- São Paulo: Prentice Hall, 2005; 

(2) STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987.

Observação: os vetores estão representados em negrito.

Interseção de Duas Retas

     Duas retas r e s coplanares e não paralelas são concorrentes. Considerando as retas: (1)

 

     Para determinar o ponto de interseção, se I (x,y,z) é este ponto, suas coordenadas satisfazem o sistema formado pelas equações r e s¹:

Resolvendo o sistema:

     Logo, o ponto de interseção das retas r e s é: I (1,-1,2).

     Exemplo:

     Verificar a ortogonalidade das retas e obter o ponto de interseção

     Igualando as expressões:

     Resolvendo o sistema:

     Logo, o ponto de interseção entre as retas r e s é: (3,0,-1). (2)

Referencias:
(1) STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;
(2) CAMARGO, Ivan de; BOULOS, Paulo. Geometria Analítica. -- 3ªed. rev e ampl -- São Paulo: Prentice Hall, 2005.

Perpendicularidade e Ortogonalidade Entre Retas

     A diferença entre retas ortogonais e retas perpendiculares é que duas retas ortogonais podem ser concorrentes ou reversas e duas retas perpendiculares são obrigatoriamente reversas. A segunda é um caso particular da primeira. (1)
     Sejam as retas r1 e r2, não paralelas, com as direções dos vetores  v1 = (a1,b1,c1) e v2 = (a2,b2,c2), respectivamente. Qualquer reta r, simultaneamente ortogonal às retas r e s, terá um vetor diretor paralelo ou igual ao vetor v1 x v2 (ilustração 5). (2)

Ilustração 5: reta ortogonal a duas retas

Fonte : retirada de (2)

     Nas condições dadas, uma reta r estará bem definida quando se conhece um dos seus pontos. (2)

     Exemplo: 

     Verifique se as retas r: x = (1,1,1) + t = (2,1,-3) e s: x = (0,1,0) + t = (-1,2,0) são ortogonais. Caso sejam, verifique a perpendicularidade: (1)
     Solução

     r = (2,1,-3) e s = (-1,2,0) são, respectivamente, vetores diretores de r e s. logo:

     (2,1,-3)∙(-1,2,0) = (2)(-1) + (1)(2) + (3)(0) = -2 + 2 + 0 = 0
     Decorre que as retas r e s são ortogonais. Vamos verificar se elas são concorrentes, para responder a segunda questão. O ponto A = (1,1,1) pertence a r, o ponto B = (0,1,0) pertence a s, e  BA = (1,0,1). Os vetores  BA, r e s são linearmente independentes, pois

     Logo, r e s são reversas. A conclusão é que são ortogonais, mas não perpendiculares.

     Exemplo: 

     Determinar as equações da reta r que passa pelo ponto A(-2,1,3) e é ortogonal comum as retas: (2)

 
     Solução
     As direções de r e s são definidas pelos vetores v1 = (-1,2,-3) e v2 = (-3,0,-1)  Então, a reta r tem a direção do vetor:

     Logo, escrevendo as equações simétricas de r, vem:

Referências
(1) CAMARGO, Ivan de; BOULOS, Paulo. Geometria Analítica. -- 3ªed. rev e ampl -- São Paulo: Prentice Hall, 2005;
(2) STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987.
Observação: os vetores estão representados em negrito.

Ponto que Divide um Segmento de Reta numa Razão Dada

     Dados os pontos  , diz-se que um ponto P(x,y,z) divide o segmento de reta   na razão r (ilustração 1) se: 

     

Ilustração 1 : ponto que divide um segmento de reta

Fonte:  retirada de 1

     Com isso, temos a equação 1: 

     Conclusão:

    (x,y,z) são as coordenadas do ponto P que divide o segmento de reta P1P2 na razão r.

     Exemplo: 

    O ponto P( 9, 14, 7) divide o segmento P1P2 na razão 2/3. Determinar P2, sabendo que P1 (1, 4, 3).

     Solução: substituindo na equação 1, pode-se obter as coordenadas de P2. Assim:

     P( 9, 14, 7) = (x, y, z), então P1 (1, 4, 3) = (x1, y1, z1) e P2 = (x2,y2, z2). Com isso temos que:

     9 = (1 - 2/3  x2)/(1- 2/3). Logo, x2  = -3;

    14 = (4 - 2/3  y2)/(1- 2/3). Logo, y2 = -1;

     7 = (3 - 2/3  z2)/(1- 2/3). Logo, z2 = 1.

     Com isso, tem-se P2 (-3,-1,1).

Referencias: 

¹ STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;

Ponto que Divide um Segmento de Reta ao Meio

     No caso de um ponto P dividir o segmento de reta P1P2 ao meio¹:

   
ou seja,   r = -1

Ilustração 1 : ponto que divide um segmento de reta ao meio

Fonte: retirada de (1)

     Equação 2:

     Exemplo:
     Dados os pontos P1 (7, -1, 3) e P2 (3, 0, -12) , determinar o ponto Q que divide o segmento P1P2 ao meio
     Solução: substituir os valores fornecidos na equação 2
     (7, -1, 3) = (x1, y1, z1) e (3, 0, -12) = (x2,y2, z2), logo, Q = (x, y, z). Utilizando a equação 2, temos que: x = (7 + 3)/2, ou seja, x = 5. Além disso, y = (-1 + 0)/2, ou seja, y = (-1)/2 e z = (3-12)/2, portanto, z = (-9)/2.
     Conclusão: Q( 5, (-1)/2, (-9)/2)

Referencias:
(1) STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;

Equação geral do plano

     Um plano π estará contido no espaço tridimensional se dado um ponto A (x1,y1,z1) e um vetor n = ai + bj + ck, n diferente de (0,0,0), tal que o vetor n seja ortogonal a todos os vetores AP, sendo P (x,y,z).

     Por definição: n.AP = 0

     Plano π:

Figura 1: Vetores AP e n representados no plano π

Adaptado de (1)

     Se n = (a,b,c) e AP= (x-x1, y-y1, z-z1) , teremos: (a,b,c)(x - x1, y - y1, z - z1) = 0

     ax - ax1 + by - by1 + cz-  cz1 = 0 , reagrupando: ax + by + cz - ax1 - by1 - cz1 = 0. Considerando -ax1 - by1 - cz1 = d: ax + by + cz = 0, definindo assim a equação geral de um plano π.

Observações:

1. O vetor n ortogonal ao plano π, quando multiplicado por um escalar k diferente de 0 irá gerar um vetor kn também ortogonal a todos os pontos contidos no plano π.
2. Sendo v1 e v¬2 dois vetores não colineares e paralelos ao plano π, o produto v1 x v¬¬2 dará origem a um vetor n que será ao mesmo tempo ortogonal a v1 e v2 e ao plano π.
3. Sendo a equação geral do plano definida por ax+by+cz+d = 0 , os coeficientes a,b e c representam as coordenadas de um vetor ortogonal ao plano, sendo assim, o coeficiente d nos permite diferencias infinitos plano paralelos entre si.

     Exemplo: 

     π 1 : 4x-5y+z+1 = 0

     π2 : 4x-5y+z+2 = 0

     Os planos π 1 e π2 são paralelos, pois dπ1 = 1 e dπ2 = 2 , sendo que ambos são ortogonais ao vetor n = (a,b,c) = (4,-5,1).

     Exemplo:

     Escrever a equação do plano π que passa pelo ponto A(3,1,-4) e é paralelo ao plano π1 : 2x - 3y + z - 6 = 0

     Sabemos que o vetor n = (2,-3,1) é ortogonal a π1 , então ele consequentemente também será normal com relação a π, pois π e π1 são paralelos.

     Pela definição: n.AP = 0. (2,-3,1)(x - 3,y - 1,z + 4) = 0. Logo, 2x - 6 - 3y + 3 + z + 4 = 0. Consequentemente, 2x - 3y + z + 1 = 0

     Conclusão: A equação do plano π é igual a 2x-3y+z+1 = 0

     Resolvendo de outra maneira:

    2x - 3y + z + d = 0, pois vimos que d é o coeficiente que diferencia dois planos paralelos. Mas como A(3,1,-4) pertence a  π, teremos que: 2(3) - 3(1) - 4 + d = 0. Logo, 6 - 3 - 4 + d = 0 e d = 1 , portanto a equação será 2x - 3y + z + 1 = 0.

Referências:

(1) STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;

Observação: os vetores estão representados em negrito.

Determinação de um plano

     Como vimos, tendo-se um ponto pertencente ao plano e um vetor ortogonal ao mesmo, podemos facilmente determinar a equação geral deste plano. Entretanto, há outras maneiras de se determinar a equação que representa um plano:

• I- Tendo um ponto A pertencente a π e dois vetores não colineares paralelos a π.

     n = v1 x v2

Figura 1: Representação de I

Adaptado de (1)

• II- Tendo dois pontos A e B pertencentes ao plano π e um vetor não-colinear a AB paralelo ao mesmo.

     n = v1 x AB

Figura 3: Representação de II

Adaptado de (1)

• III-  Tendo três pontos não pertencentes a uma mesma reta.

Figura 4: Representação de III

Adaptado de (1)

• IV- Tendo duas retas que se intersecionam, e os vetores diretores das mesmas.

     n = v1  x v2

Figura 5: Representação de IV

Adaptado de (1)

• V- Tendo duas retas paralelas, um ponto pertencente a cada uma das duas e o vetor diretor de uma delas.

     n = v x A1A2

Figura 6: Representação de V

Adaptado de (1)

• VI – Tendo uma reta pertencente ao plano, o vetor diretor da mesma, um ponto A pertencente a r e um ponto B não pertencente a r.

     n = v1  x AB

Figura 7: Representação de VI

Adaptado de (1)

     Como pode-se observar, em todos os casos a determinação de um vetor n normal ao plano fica em função do produto externo entre dois vetores pertencentes ao mesmo, então utilizando este raciocínio, chamamos estes vetores de “vetores-base”.

     Exemplo:

     Estabelecer a equação geral do plano determinado pelos pontos A(2,1,-1) , B(0,-1,1) e C(1,2,1).

     Como vimos em III, os três pontos pertencem ao plano e não formam uma reta, portanto, podemos fazer o seguinte produto: n = AB x AC:

     Como A, B e C pertencem ao plano, podemos montar a equação geral utilizando qualquer um dos três pontos. Vamos considerar o ponto C: n.CP = 0 , sendo P(x,y,z)

     (-6,2,-4)(x - 1,y - 2,z - 1) = 0. Com isso, -6x + 6 + 2y - 4 - 4z + 4 = 0, resultado em -6x + 2y - 4z + 6 = 0

     O ponto de interseção entre a reta r e o plano π é (-2,-1,-10).

Referências:

(1) STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson Makron Books, 1987;

Observação: os vetores estão representados em negrito.